Amdahl定律
概述
Amdahl 定律(Amdahl’s law)是并行计算领域一个非常著名的定律。由 Gene Amdahl 于1967年提出。Amdahl 定律描述的是数据规模固定时,渐进加速比的变化趋势。
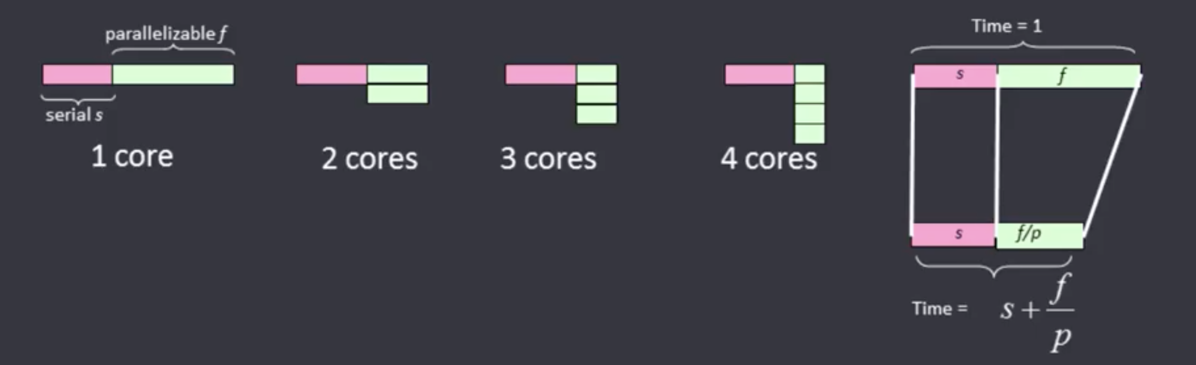
$$Time = s + \frac{f}{p} $$
- $s$ 串行部分
- $f$ 并行部分
- $p$ 核数
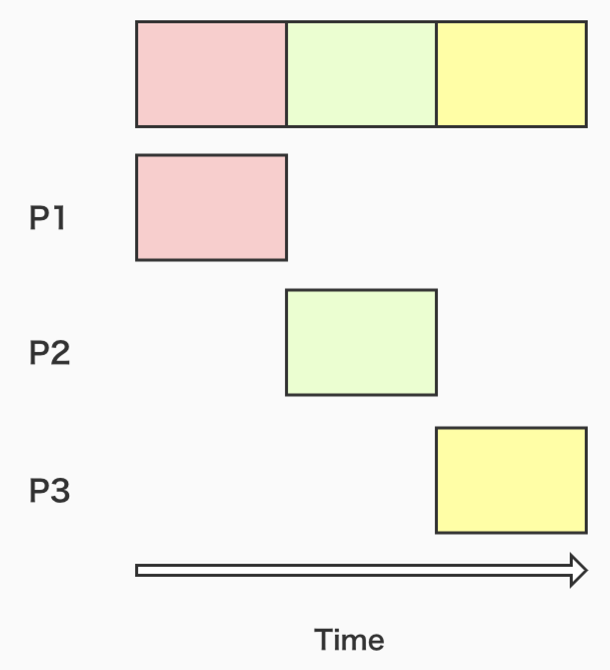
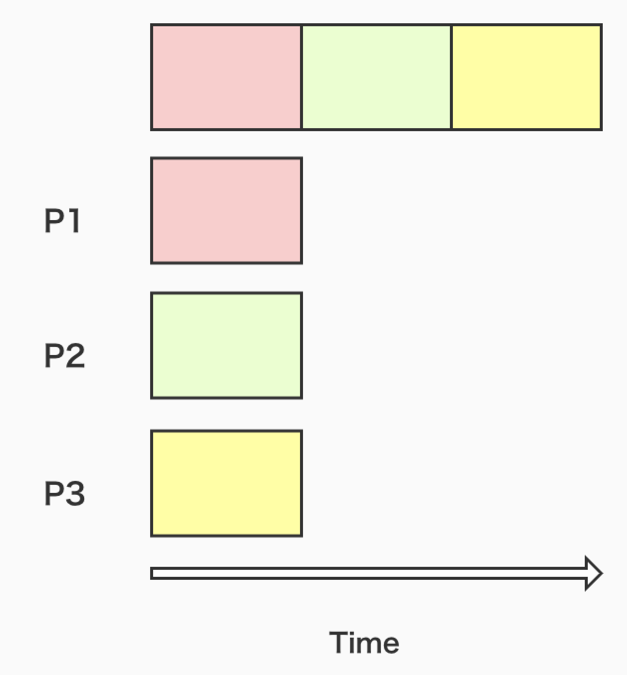
如下图所示。
介绍
假设我们有一个任务 task 里有25%的代码是并行的。那么在单机多核的情况下,我们可以获得怎样的加速比呢?
- $i$ 核数
- $m_{i}$ 有用 $i$ 核数的机器
单机单核的效率。
$$m_{1} = 25% + 75% = 100% $$
单机双核是单机单核的 $\frac{7}{8}$。
$$m_{2} = 25% \times \frac{1}{2} + 75% = \frac{7}{8} $$
单机4核是单机单核的 $\frac{13}{16}$。
$$m_{4} = 25% \times \frac{1}{4} + 75% = \frac{13}{16} $$
单机8核是单机单核的 $\frac{25}{32}$。
$$m_{8} = 25% \times \frac{1}{8} + 75% = \frac{25}{32} $$
单机1000核是单机单核的 $\frac{3001}{4000}$。
$$m_{1000} = 25% \times \frac{1}{1000} + 75% = \frac{3001}{4000} $$
单机无数核是单机单核的 $\frac{3}{4}$。
$$m_{+\infty} = 25% \times \frac{1}{+\infty} + 75% = \frac{3}{4} $$
从以上推算,可以知道,当并行代码所占的百分比固定的情况下,随着核数 $i$ 增加,对并行效率的提升会固定在一定比例。
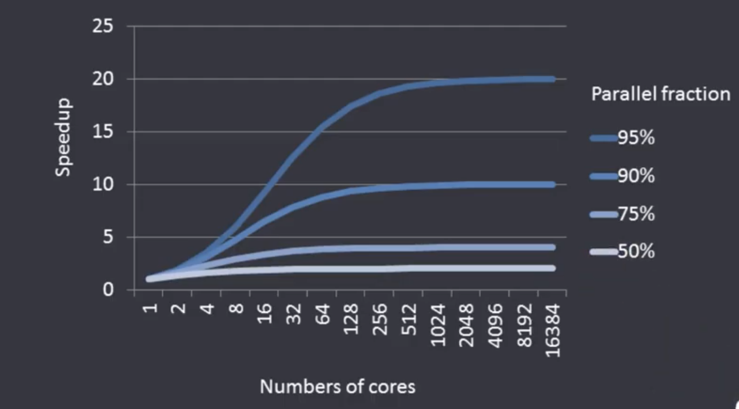
总结
Amdahl 定律假设的是输入的数据规模是固定的,这与 Gustafson 定律的假设是不一样的,下一篇会讲讲 Gustafson 定律,并且解释一下两者之间的异同。
参考资料
- Introduction to HPC with MPI for Data Science
- https://www.youtube.com/watch?v=ViMI_ciiC2A
- https://www.youtube.com/watch?v=Axx2xuB-Xuo